746346

Previous Page

Next Page

Page Background

.,

Liber

l.

669;

,a

cortvexitatem nullamque-ibi refcal\ionem p•–

r!emt,ergo ica

proci:dec-ac

li

veniret

ex

puni:\o

C,

e

C O R O L L AR 1UM

l.

Si cadem menifcus obverrerer convexitatem

ad lucidum , ita

Cfl

t

C

d1fferencia Íemidi2me–

trorum

ad CD

ÍCc1H·l:a1uecrum convexi, ut dupla

AE,

íeu CA ad diftandatn foci; íed primus

&

tcr–

tius terminus a:qua!es funt; ergo íccundus ,

&

1

c¡uartusa:qu2les enmt. Eritque focus in diíl:ancia

femidia'11etri convexi. Qu•re pw ..de

efi

quam–

ounque fociem ad lucidum obverras.

C O R O L L

A:

R l U M

Ú.

'Regula gencralis cíl:o pro omnibus Ípha:ricis

urrinq

•e

fpecillis. Si Ípha:ricitates lint oppolicz

fau in divcrfas partes,rcípicianc, fiar, ut aggrcga–

rnm femidiamecrouum 2d 2lterutram íem1diame–

trum, ita altera diamerer integra acl diíl:anriam

fuci.

Vel ur aggregttum diamerrornm ad unam dia–

mecrum', ita alta d1amerer ad diíl:anriam

foci,

li

fphairitarcs linr obverÍ:<: in eandem partem, ira

erir difíeremia (emidiametrorum ad fcmidiame–

rrum con.vexiiarls , ira diameter integra ad di–

ftantiam foci.

Ve\

ut

differentia diametrorum ad unam dia–

metrum, ica alia diamercr ad d1!bmiam foci.

11f1li!ll1!!7il\'l.!l11!!%<tf.!Q!!00®.'!1l!'J5Jfll):lit)~!l.!lll!!ltll!fl:l.!!

PROPOSlTIO XXXJ.

Theorema.

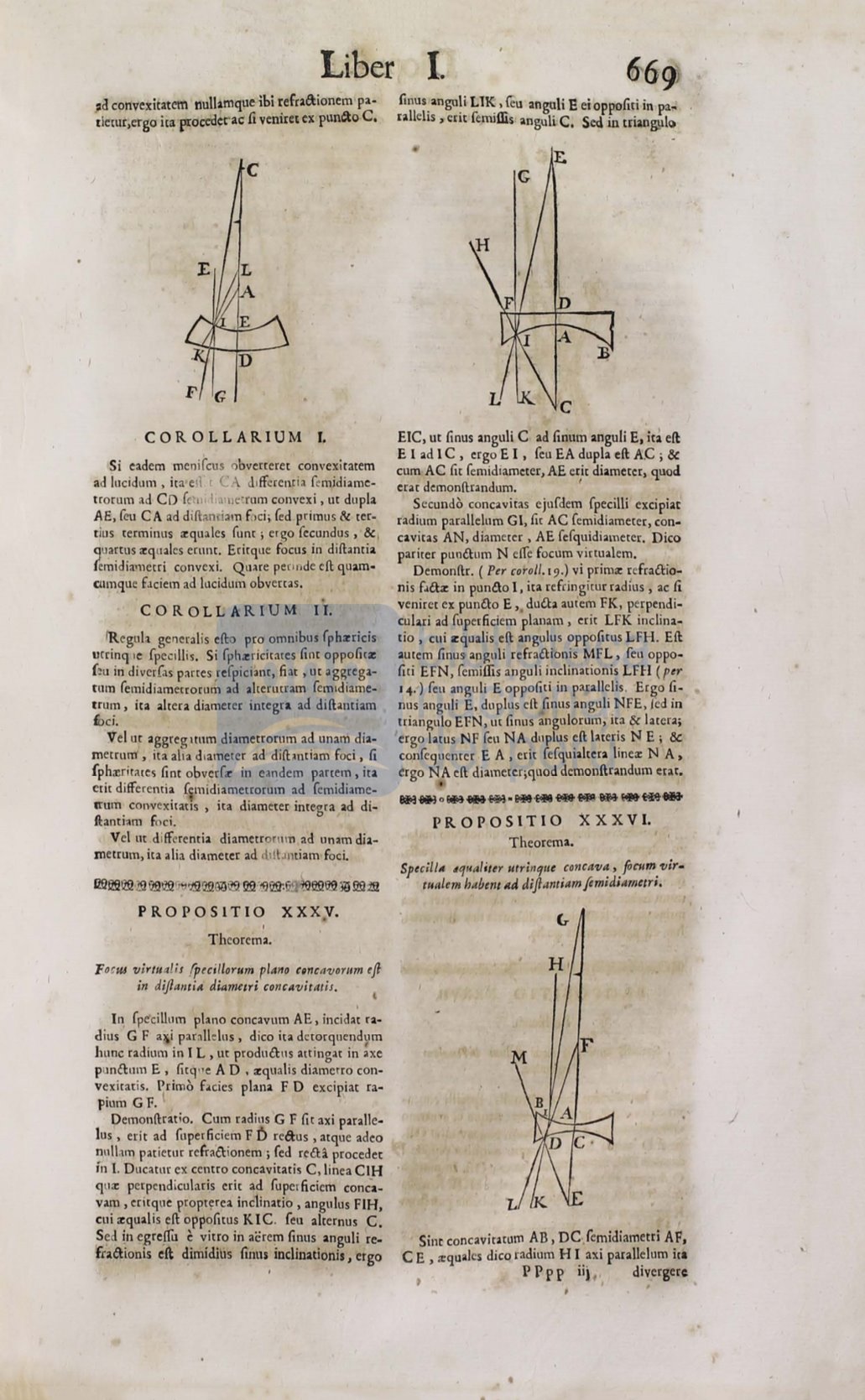
Focm virtua/;s (pecillorum plano c.ncnvorum

eft

in dif/anti11 diameeri

conc4vitatis.

1

In

Ípe'cillum plano concavum AE,

incida~

ra–

dius G F

ª"¡

parallelus, dico ira derorquend¡1m

Jume radium in

1

L , ut produll:us atringar in axe

punll:um E , fitqnc A D , a:qualis diametro con–

vexiratis. Primo facies plana F D excip,iat ra-

pium GF. l

·

Demoníl:ratio. Cum radius G F lit axi paralle–

lus , erir ad fuperficiem F

D

redus , arque adco

~llllam

parierur refraél:ionem ; fed rell:a proceder

111

l.

Dllcatur ex centro concaviraris C, lineaCIH

qua: perpcndicularis erit ad fuperficicm conc"a–

vam, crirquc

propr~rea

inclinaría, angulus FIH,

cui a:qualis eíl: oppolirus KIC. feu alcernus C.

S~d

in egrcffu

e

viera in acre!"' linus anguli re–

fraél:ionis el\ dimícliüs fmus. inclinationis, ergo

linus.anguli Lll<'., feu anguli E eioppoli.ti in pa,:

ullehs

'em

fcmJilis anguli

C. Sed

anwl<>

EIC,

ut linus anguli

C ad

linum anguli

E,

ira eft

E

1

ad IC , ergo E

1 ,

fcu EA dupla cíl: A.C ;

&

cum AC lir íemid1amcrer,A.E erit diamercr, quod

crac dcmoníl:randum.

1

Secundo concaviras ejufdem fpecilli excipiar

radium parallelum GI,

lic

AC femidiameter, con–

caviras AN, diamercr , AE ícfquidiamerer. Dico

pariter punll:llm N

elfe

focum vircualem.

Demoníl:r. (

Per coro//.

19.)

vi prima: refrall'io–

nis

f.ill:a:

in punélo

l,

ira refringítur radius , ac

li

venirerex punél:o E>. dull:a auiem FK, perpendi–

culari ad fuperficiem planam, crit LFK inclina–

tio , cui zqualis

en

angulus oppolirus LFH. Eíl:

~ucem

linus anj!;tili refrall:ionis MFL, feu oppo–

lici

EFN, femiffis anguli inclinarionis LFH (

per

1

4.)

fcu anguli Eoppofiti in parallelis. Ergo li–

nus anguli E, dnplus cíl: linus anguli NFE, fed

in

triangulo EFN, ur linos angnlorum, ira

&

latera;

'ergo larus NF fcu NA duplus eíl: bteris NE; llG

co¡1fequenrcr E A , erir fefquialrcra linea: N A,

ergo Nf cíl;·diameccr;quod demonfirandum crac.

e.l@lo!fiiM~•M&fft-- ·QNl4&tfitiMo

PROPOSlTIO XXXVI.

Theorema.

Specil/11

1qualiier utrin911e concava,

focum

vir–

tualem

habent

11d

diftantiamftmidiametri.

Sinr concavirarurn AB, OC femicliametri AF,

CE , a:quales dico radium H

1

axi parallelum ita

>

P P p p

iii ,

diverger~

J