
Liber
lll.'
LIBE R
TER T 1 V
s.
!ltl!lBll1!1lílll1!1líl!lM1.!ll1!iJt\00'1lllll1!10011!lltHil!OO!l:il!l1.11.l'ii
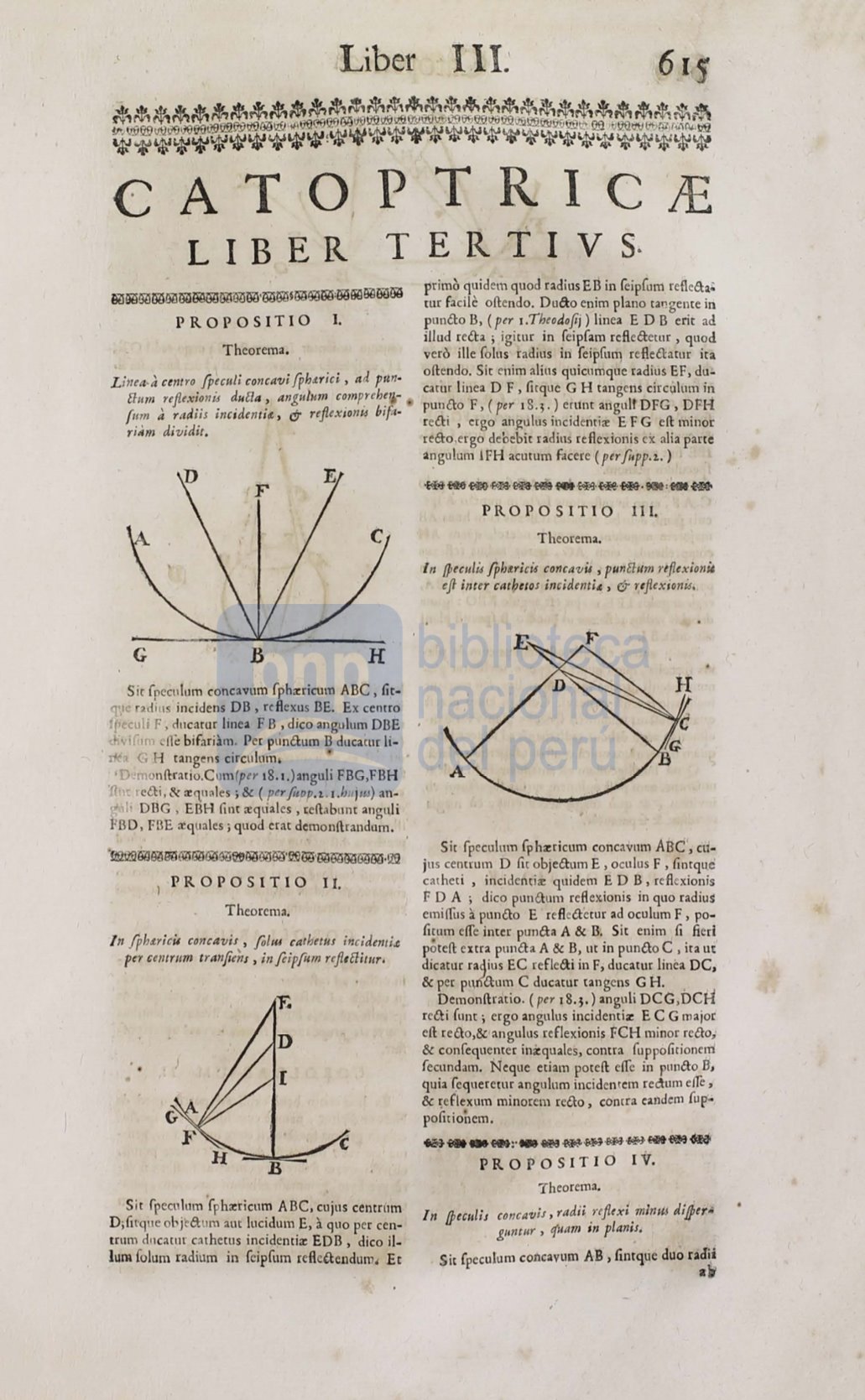
P R O P O S IT 1O l.
Theorema.
Linea-a centro fpuuli concavi
fph~rici
,
ad pt<n·
El:um reftexionu duEla
,
angulHm
comp.reh~r¡.ftm•
a rt11iiis incidenti.t,
&
rejlex1onu
bifa·
riJm dividir.
G
B
H
Sir foecnlum concavnm fph:rricum ABC, lir–
q•.1e
radlus incidens DB, rdlexus BE. Ex centro
Íf•eculi F, dncarur linea F B.' dico angulum DBE
.vifom
~fli:
bifariam. Per punél:um ll ducaeur li-
. tk• (,
H tangcns circult1m,
•
•D ..moníl:ratio.Cum(per 18.1.)anguli FBG,FllH
"fht reél:i,
&
:rqnoles;
& (
per
fi•Pp. i .
t.lmjr>J) an–
¡. DBG , EBH finr reqtiales , refhbtmr anguli
·BD, FllE :tquales; quod erar dcmoníl:randam.
"!i!WliÍ"llll1!00@1ltiilll!li:l~OOiJt\1lll'll.!llliJ·Ni¡¡¡¡!!lltilllll:i·!Zli
l
PROPOSITIO 11.
Theorema.
In
fph.tricú concavi1,
fol"'
cathetu1 incidemi.e
per
cemrmn tranfiens, in flipfi<m rejl1éliwr.
Sir Ípeculum Ípha:ricum ABC, cujus centrúm
D;litque
obj~éh1m
aut lucidum E,
a
quo per cen–
trum dncarur cathetus incidentia: EDll , dico il–
lum folum radium in fcipíum reflcllendum, Er
primo c¡uidem quod radius EB in íeipfom refleél:ai:
rur facilc oíl:endo. Duél:o enim plano
m~gence
in
punél:o B, (
per i.Theodofij)
linea E D B erir ad
illud reél:• ; igitur in feipíam rcfleél:emr, quod
vero ille íolus radius in feipfmri refleél:arur ira
oíl:endo. Sír enim alius quicumque radius EF, du–
camr linea D F , firquc G H rangens circulum in
punél:o
F,(per
18.¡.) entnt angnllDFG, DFH
reél:i , ergo angulus incidentire E FG eíl: minor
reél:o,ergo debebir radius reflexionis ex alia parte
a~gulum
lFH acumm facere
(per
fi•PP·")
~-~-.e!F&ff!!Mffl·M>e-N>!l·Ql'€Gt~
PROPOSITIO lll.
Theorema.
l
n
1Jec11lu
fph~rici4
concavu
,
punf111m njlexionu
eft in.ter
cat~etos
incideml,
,
&
reflexionu..
Sic ípeculnm Ípha:cicum concavnm
ABC',
etl–
jns cemrum D
lit
objeél:um E, ocnlus F , fincqu.e
catheti , incidenrire quidem E D B , reflexionis
F D A ; dico punéhun reflexionis in quo radius
emiffos
a
punél:o E refleél:ecur ad oculum F, po–
licmn
elfe
inrer punél:a A
&
B. Sit enim fi fieri
pÓteíl: exrra punél:a A
&
B,
ut
in punél:o C, ira ut'
dicatur raqius EC refleél:i in F, ducatur linea DC,
&
per pt1rfél:um C ducarur rangens G H. .
Demoníl:rario. (
per
18.¡.) anguli DCG,DCfi
relH
fonr ; ergo angnlus incidentiz E C Gmajor
eíl: reél:o,&•angulus reflexionis FCH minor reél:o;
& coníeque,mer inzquales, comra fuppolitionem
fecnndam. Ncque eriam poreíl:
elfo
in punél:o g,
quia íeqneremr angnlnm incidenccm redum elfe,
&
~eflexum
minorem reél:o, conrra candcm
fo¡t·
pofitionem.
~ililte&-:·Nl&@<'l.--m.m#>)Hit~*"'
p
R
o
p
o
S I T I O 1
V.
7heorema.
In f}eculiJ concaviJ, radii nflext mln11J
di¡fer~
guntur
,
'Í"ª"'
in plani1.
Sit fpecufum
c~ncavum
AB, Jinrque duo radi,í
.
alJ
















