746346

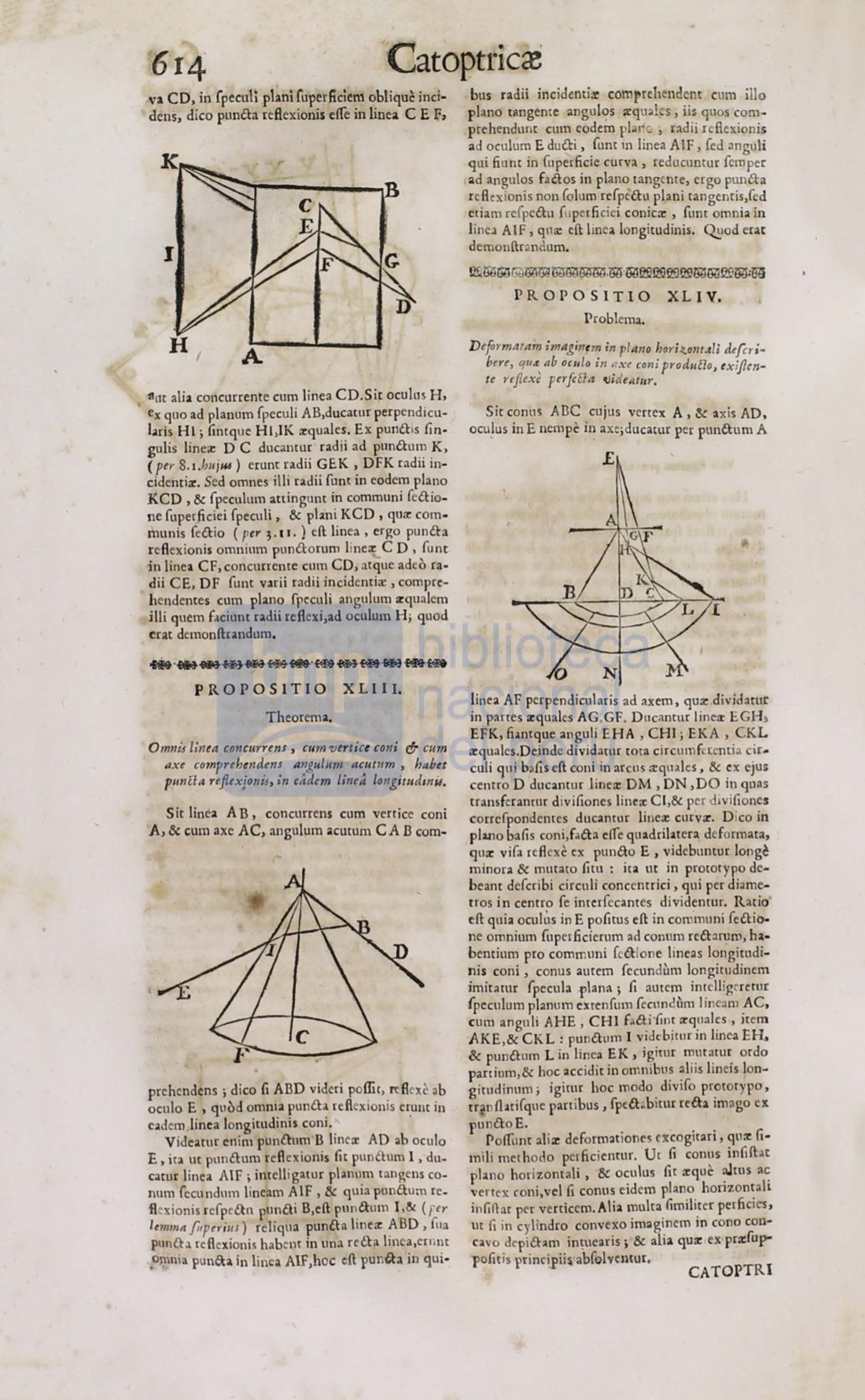
Gat0ptrici

va CD, in fpeculi plani fuperliciem obtiquc inci–

dens, dico punél:a ref!exionis

elfe

in linea C E F,

ªm

alia concurrente cum linea CD.Sic oculus

quo ad planum fpeculi AB,ducacur perpendicu–

laris HL; !imque Hl,IK "'quales. Ex punél:1s !in–

gulis line"' D C ducamur radii ad punél:um K,

( per

8. 1.h11j1U)

erunt radii GE.K, DFK radii in–

cidenti:r. Sed omnes illi radii funt in eodem plano

KCD , & fpeculum attingum in communi feél:io–

ne fuperficiei fpeculi, & plani KCD, qu"' com–

munis feél:io (

per

. 11. )

efl linea , ergo punél:a

ref\exionis omnium punél:orum line31 CD, funr

in linea CF,concurrente cum CD, arque adeo ra–

dii CE, DF

funt

varii radii incidcntire , compre–

hendemes cum plano ípeculi angulum :rqualem

illi quem faciunt radii ref\exi,ad oculum H; quod

erar demonflrandum.

---~-@ó}-~i!M-·ff&f!f4@eo~fftffi

PROPOSITIO XLIII•.

Theorema.

Omni& linea conc11rren1, c11mvertice co11i

c11m

axe comprehenden1

1111g11IH1n

arnmm

habtt

punfla rejlexjonu,

cíidem line/i longit11dmu.

Sir linea A B, concurrens cum venice coni

A, & curn axe AC, angulum acutum CA

corn-

prehendens ; dico

ABD videri poffic, rrf!exe ab

oculo E , quod omnia punél:a reflexionis erunt in

eadem linea longicudinis coni.

Vidcarnr enim punlh1m B linc"' AD ab oculo

ica ut punél:um reflexionis

!ic

punél:um

du–

carnr linea AIF; imelligatur planum tangens co–

num fecundum lineam AIF , & quia ponélum re.

flexionis refpeéln punél:i B,ell ptrnél:um I,&

( per

lemma

f1peri111)

reliqua punéh !mere ABD , Ít1a

punlh reflexionis habenr in una reél:a linea,ernm

•

o~mia

punaa in linea AlF,hoc efl punll:a in qui-

bus radii incidenti:r comprehendem cmn illo

plano tangente angul?s requalcs, iis quos com–

prehendunt cum eodem planc , radii ref!exionis

ad oculum E duél:i , fum

linea Alf, fed ang11li

qui fium in íitperficie curva, reducuntur fcmper

ad angulos faltos in plano rangmre, ergo punél:a

refüxionis non folum refpelht plani rangentis,fcd

etiam refpcél:u fuperficici conicre ,

lime

omnia in

linea

AlF,

qua: efl linea longitudinis.

~od

erat

demonnrandum.

!lí11.fll~G!l1JlllJ.q!l!l1J!!1Jll1lll,1Jll·1lllll:!ll1.fll1.fl!i!lllflllfll1.fl1lli:OO

PROPOÚTIO XLIV.

Problema.

Deformaram imAgin,m i

n pla

hori~om:ili

deferí•

bere,

q114

11b

oculo in

11.xe

coni produ[fo,

exifl.en–

ujlexe perfofla 'Uideatllr.

Sic conus

BC cujus verrex A,

axis AD,

ocu}us in E nempe in axe;ducacur per punél:um

linea AF perpendicularis ad axem, qu"' clividamr

in parres "'quales AG,GF. Ducantur linere EGJ;I,

EFK,fiamqueanguli EHA , CHl ; EKA,

CKL

a:quales.Deinde dividatnr roca circumfcrentia cir·

culi qui ba!is efl coni in arcus a:quales ,

ex ejus

centro D ducamur linere DM ,

,DO in quas

transferanmr divi!iones linc"' CI,& pcr diviliones

corrcfpondentes ducamur line"' curv:r. Dico in

plano ba!is coni,faél:a

elfe

quadrilatera deformara,

qu"' vifa rellexe ex punél:o E , videbumur longe

minora & mutaro lim : ica

in promrypo de–

beanr defcribi circuli concemrici, qui per diame–

tros in centro fe imerfecames dividencur. Ratio

efl quia oculus in

policus efl in communi feél:io–

ne omnimn fuperficiernm ad conum reél:arum, ha–

bencium pro communi fe&ione lineas longitudi–

nis coni , conus aucem fecundum longicudinem

imitamr fpecula plana ;

aucem inrclligcrerur

fpcculum planum exrenfum fecundum lineam AC,

cum anguli AHE , CH! faél:d int requales , frem

AKE,& CKL : punél:um I videbimr in linea

EH.

punél:mn

in linea EK, igicur mmarur ordo

panium,& hoc accidit in omnibus aliis lineis lon–

girudinum; igimr hoc modo divifo prototypo,

u~nflatifque

parcibus, fpell:abirur reéb imago

punll:oE.

Po!Tim t alire deformat1ones excogitan , qua:

(j.

mili mec hodo perficienmr.

!i conus inliftat

plano horizonrali , & oculus !ic reque :Jms

vercex coni,vel

conus eidem plano honzontah

in!iflat per verticern.Alia multa Ílmiliter perficies,

in cylindro convexo imaginem in cono con–

cavo depiél:am in¡uearis; & alía qua: ex·prrefup–

l'olitis

princ~iis

abfolvemur•

CATOPTR l