
I
DE ASTRONOMJA,.
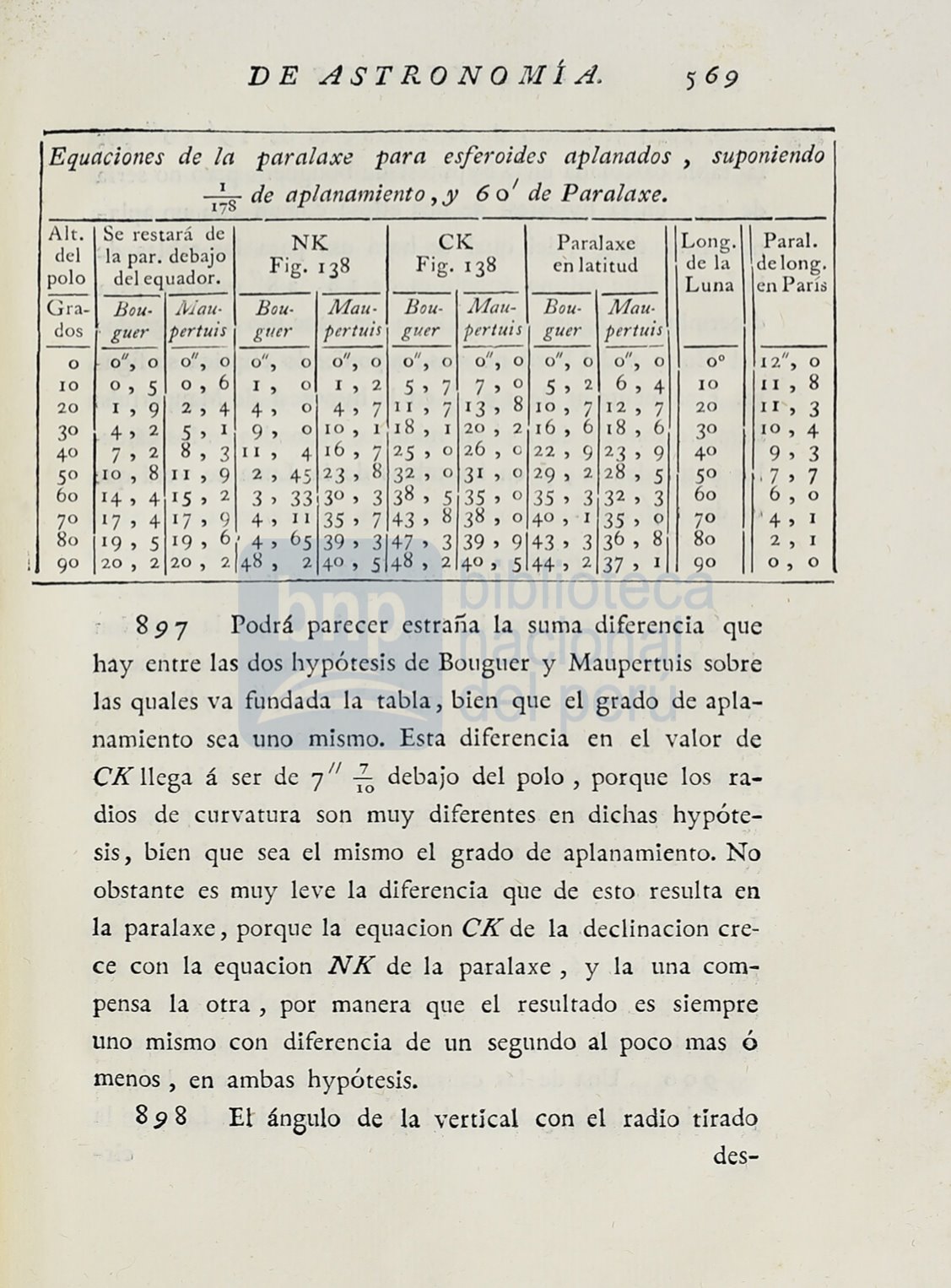
Equ~ciónes de
la
paralaxe para esferoides aplanados
,
suponiendo
+s
de aplanamiento,
y
6 o
1
de Paralaxe.
polo
del equador.
NK
Fig.
138
Gra-
Bou-
Va;;
Bou-
Mau-
B ou-
·
Mau-
Paralaxe
en
latitud
Bou-
Mau-
Alt. ¡Se restará de
del
: la par. debajo
dos
r
guer pertuis
guer
pertuis guer
_pe_r,_u_is
guer
pertuis
o
ºu'
o
0
11
,
o
0
11
'
o
0
11
'
o
0
11
'
o
o:',
o
0
11
'
o
0
11
'
o
IO
O
,
5
O
,
6
I
,
O
I
,
2
5
, 7
7 ,
O
5
,
2
6
,
4
20
I
,
9
2
,
4
4 ,
O
4 ,
7
I I
,
7
I
3 ,
8
I O ,
7
I 2
,
7
30
4 ,
2
5 ,
I
9 ,
O
I O ,
I
I
8 ,
I
20 ,
2
I
6 , 6
I
8 , 6
40
f
7 ,
2
8 , 3
I
l
,
4
16 ,
7
25 ,
O
26 ,
22 ,
9
23 ,
9
50
IO,
8
II,
9
2,
45
+3, 8
32,
O
31 ,
O
29,
2
28,
5
60 14' 4 15 '
2
3 ' 33 3º ' 3 38 ' 5 35 '
o
35 ' 3 3
2
'
3
70
I
7 ,
4
17 ,
9
4 ,
I I
35 ,
7
43 , 8
38 ,
O
40 , 1 35 ,
O
80
¡19,
5
19'
61·
4'
65 39'
3/47,
3 39'
9143' 3
36'
811
90
20 '
2
20 '
2
48 '
2
40 '
5·
48 ,
2
40 ,
5
44 '
2
37 '
1
Long. \ Paral.
de
la
delong.
Luna
en
París
oº
12
11
,
o
10
II,
8
20
I I
,
3
3º
!º, 4
4º
9' 3
5º
1
7 ' 7
60
6'
o
70
.1
4'
I
80
2, I
90
o, o
~
8
9
7
Podrá
parecer estraña la suma diferencia que
hay
entre las
dos hypótesis
de
Bouguer y Mauperruis
sobre
las quales va
fundada la tabla,
bien que
el grado
de
apla–
namiento sea uno mismo. Esta diferencia en
el
valor de
CK
llega
á
ser
de
7
11
;
0
debajo
del
polo , porque los
ra–
dios de .curvatura son muy diferentes en dichas hypót~–
sis, bien
que
sea
el
mismo
el grado
de aplanamiento.
No
obstante es muy leve la diferencia que de esto resulta en
la
paralaxe, porque la equacion
CK
de la .declinacion
cre–
ce
con la equacion
N K
de la paralaxe ,
y
.la
una
com~
pensa la otra , por manera que
el
resulra~o .es siempr~
uno
mismo
con
diferencia
de un
segundo al
poco
mas
ó
menos , en ambas hypótesis.
8
9
8
El ángulo de la :vertical
con
el
radío tiradq
des-
\














