
ELEMENTOS.
Fig.
ro esto se remedia por
el
método
indirecto (
-6 9
6 ).
La
tabla s_iguiente
se
calcúla por lo dicho (
4
6
y
5 o).
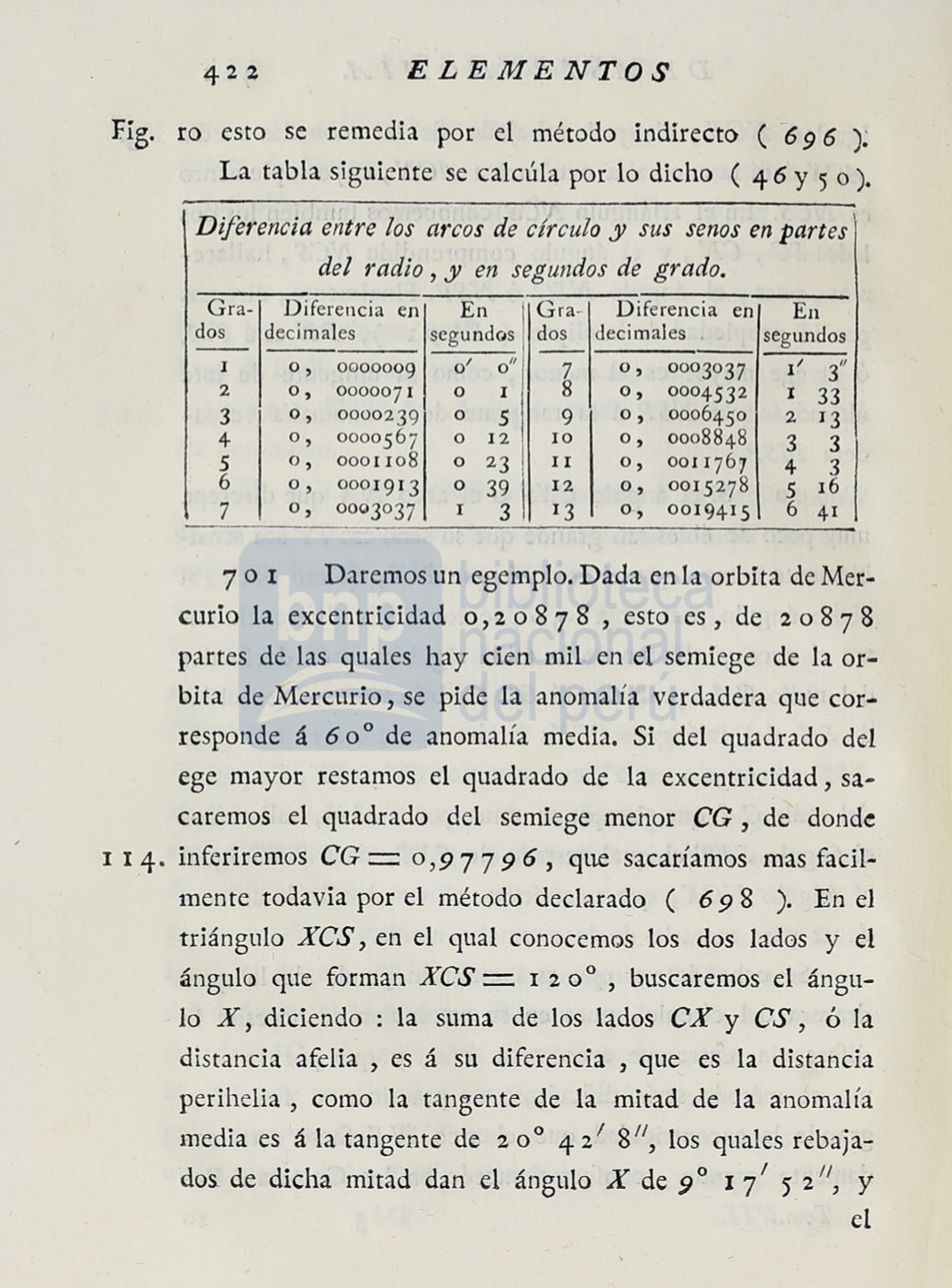
Diferencia entre los arcos de círculo .Y sus senos en partes ·
·
del radio,
y
en segundos de grado.
Gra-
Diferencia en
En
· Gra
Diferencia en
En
dos
decimales
segundc.,s
dos
decimales
segundos
I
o,
0000009
o'
o''
7
o,
0003037
1/
3"
2
o,
0000071
o
I
8
o,
0004532
I
33
3
o,
0000239
o
5
9
o, .
0006450
2
13
4
o,
000056 7
o
12
IO
o,
0008848
3
3
5
o,
0001108
o
23
lI
o,
oon767
4
3
6
o,
0001913
o
39 ·
12
0,
0015278
5
16
7
o,
0003037
I
3
13
o,
0019415
6
41
701
Daremos un egemplo. Dada en
la
orbita de
Mer-
curio
la
excentricidad o,
2
o
8 7 8 ,
esto es , de
2
o
8 7 8.
partes de -las. quales
hay
cien mil en el semiege de la or–
bita de Merc_urio, se pide la anomalía verdadera que cor–
responde
á
6
oº de anomalía medía.
Si
del quadrado del
ege mayor restamos el quadrado de la excentric~dad , sa–
caremos
el
quadrado del semíege menor
CG
,
de donde
1 I
_4·
inferiremos
CG
==
0,9
7 7
9
6,
que sacaríamos mas facil- ·
mente todavia por el método declara4Q (
6 9
8
).
En el
triángulo
XCS,
en
el qual conocemos los dos lados
y
el
1
ángulo que forman
XCS
==
1
z
o
O
. ,
buscaremos el ángu-
- lo
X,
diciendo : la suma de ·
los
lados
CX
y
CS
,
ó
ia·
distancia afelia , es á
su
diferencia ,
que
e~ la distancia
perihelia , como la tangente de la mitad de la anomalía
media es á la tangente de
2
o
O
42
1
8
11 ,
los quales rebaja–
dos.
de
dicha mitad dan
el
ángulo
X
de
9°
I
7
1
5.
2 11
,
y
. . el














